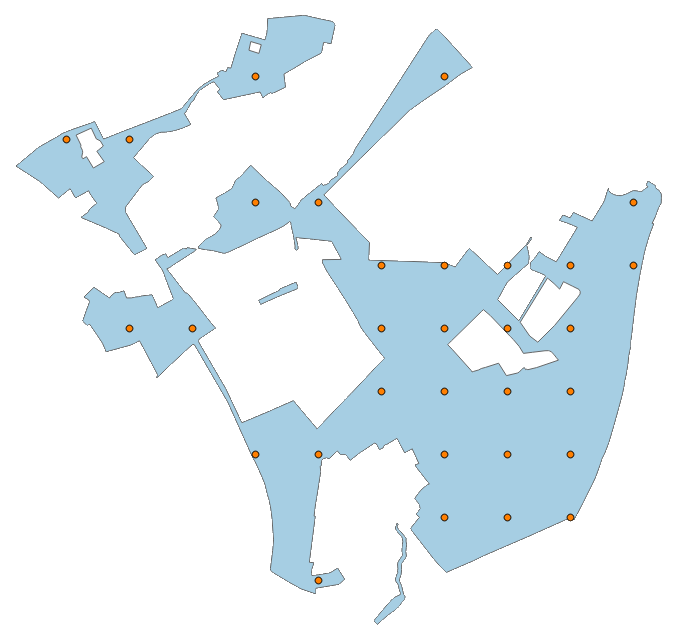
The third edition of this series will introduce a more complex sampling method to create points that are spread both randomly and uniformly over the area of a given source polygon.
Previously published parts of this series include:
Uniform random sampling
To distribute points in a polygon in a uniform and random manner we are going to follow an approach laid out within the scope of a discussion amongst MATLAB users. In case the internet will forget this minor thread someday, here’s the reduction of the problem as laid out by merited forum contributor John D’Errico:
“[…] the general approach […] that generates uniform random points inside a general object in n-dimensions.
“Compute the area/volume of each simplex, then assign points to them randomly with probability defined by their area relative to the total area. Within each simplex, […] use a […] method of generating random points […].
“Of course, you need a triangulation of the polygon, but as long as the polygon is a convex one, this is trivial with [D]elaunay.”
To summarize these are steps necessary to create uniform random points in a polygon:
- Use the polygon’s vertices to create a Delaunay triangulation. As we can’t guarantee that real-world data will only contain convex geometries, this needs to be generalized form of it, a constrained Delaunay triangulation.
- Use the area of each created triangle to create a weighted random selection, i.e. to assure that larger triangles a picked more likely than smaller ones.
- Randomly create a point inside the selected triangle.
Now these procedure shall be repeated until a certain stop criterion is fulfilled, something that we will discuss later on. Let’s start with triangualation first.
Delaunay triangulation and constrained Delaunay triangulation
Whilst the original (C++) OGR library contains a method DelaunayTriangulation to retrieve just that for an input geometry, this function is not part of the OGR Python bindings. However, as with most tasks there is already another library that can do what we want. In this case we refer to poly2tri. Originally provided in Java and C++, there also exists a Python version of it. (There are some peculiar patches necessary to get poly2tri to work under Python that I will devote another blog entry for.)
Using Shapely and poly2tri it is now possible to initiate a constrained Delaunay triangulation (CDT):
>>> # creating a source polygon first >>> from shapely.geometry import Polygon >>> from shapely.wkt import loads >>> polygon = loads(open(r"real_world_data.wkt").read()) >>> # preparing list of vertices and adding those of current polygon to it >>> vertices = list() >>> for coord_pair in polygon.exterior.coords: ... vertices.append(coord_pair) >>> # p2t is the Python module name for poly2tri >>> import p2t
Now two things have to be considered. First, poly2tri brings its very own Point definition that needs to be distinguished from the one Shapely provides by explicitly using the prefix p2t. Adding to that it must be avoided that the CDT is fed with duplicate points – i.e. as first and last vertex are usually specified in polygon definition. We can deal with this constraint by omitting the first vertex:
>>> # making sure that only one of first or last vertex >>> # is used to create list of input points for triangulation >>> border = [p2t.Point(x, y) for x, y in vertices[1:]] >>> # setting up constrained Delaunay triangulation >>> cdt = p2t.CDT(border)
Now real-world data kicks in back again as it may contain holes, or interior rings as they are called correctly. These need to be specified separately as input for the CDT:
>>> for interior_ring in polygon.interiors: ... hole = list() ... for coord_pair in interior_ring.coords: ... hole.append(coord_pair) ... else: ... cdt.add_hole([p2t.Point(x, y) for x, y in hole[1:]])
Finally, the triangulation can be performed:
>>> triangulation = cdt.triangulate() >>> print len(triangulation) 1964 >>> for t in triangulation: ... triangle = Polygon([(t.a.x, t.a.y), (t.b.x, t.b.y), (t.c.x, t.c.y)]) ... print triangle ... POLYGON ((366392.3774440361 5640960.820684713, 367546.1057238859 5641233.076879927, 366393.6058517902 5641064.830985503, 366392.3774440361 5640960.820684713)) POLYGON ((366393.6058517902 5641064.830985503, 367546.1057238859 5641233.076879927, 367452.1526190441 5641333.95416048, 366393.6058517902 5641064.830985503)) ... ...
Following is the visual result of the triangulation.
Next up in line to create uniformly random sample points are weighted random selection of triangles and random generation of points inside such a given triangle.