Monthly Archives: January 2015

Creating sample points (Pt. 1): Centroids and representative points

Leave a reply

Following the declaration of my PolygonPointSampler’s base class in the previous post, I will now start to implement multiple classes each representing a different method to derive sample points for a given polygon.

Centroid sampling

Let’s start with the simplest polygon-to-point sampling method available: the creation of a centroid point. The centroid represents the geometric center of a polygon. If we’re looking at a triangle it emerges as the intersection of the triangle’s median lines, hence it is sometimes also called the median point. Shapely allows to derive a polygon’s centroid by querying the corresponding attribute:

>>> from shapely.geometry import Polygon
>>> polygon = Polygon([(0,0), (6,0), (0,6)])
>>> centroid = polygon.centroid
>>> print centroid
POINT (2 2)

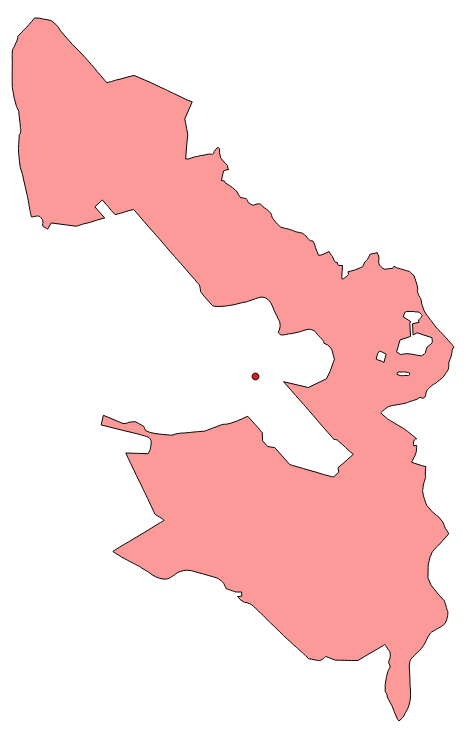
Applying this method to some real-word data will often lead to the phenomenon visible below: The centroid comes to lie outside of the original polygon’s interior.

A real-world polygon with a sampling centroid.

Representative point sampling

To deal with this problem, Shapely equips geometry objects with a method called representative_point() that – as the documentation reads – “returns a cheaply computed point that is guaranteed to be within the geometric object”. Judging from the Shapely source code this method goes back to the PointOnSurface function provided by GEOS. I haven’t been able to find out how exactly it is guaranteed that the sample point is an interior point, but from the looks of it, it is most likely that the algorithm described in a fitting thread at gis.stackexchange.com has been applied to it. In any way for our Python example the code would look like the following:

>>> representative_point = polygon.representative_point()
>>> print representative_point
POINT (1.5 3)

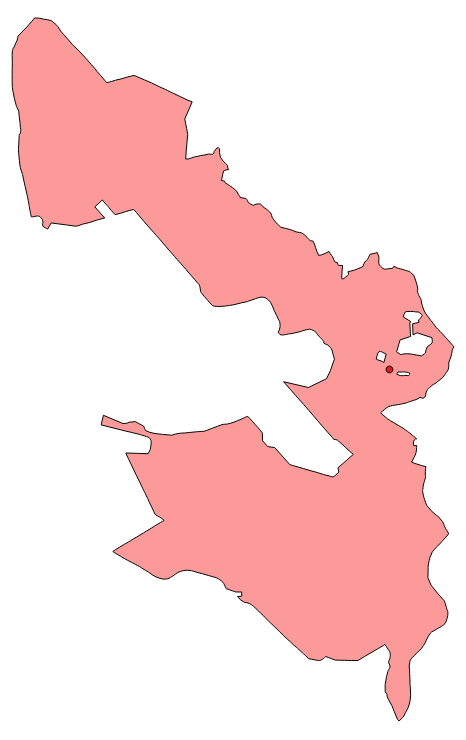
Please note that querying for the representative point of a polygon actually calls a Python function – as indicated by the brackets following the according declaration – while the centroid is a property of the Shapely polygon object. Using real-world data we arrive at the situation displayed below:

A real-world polygon with a sampling representative point.

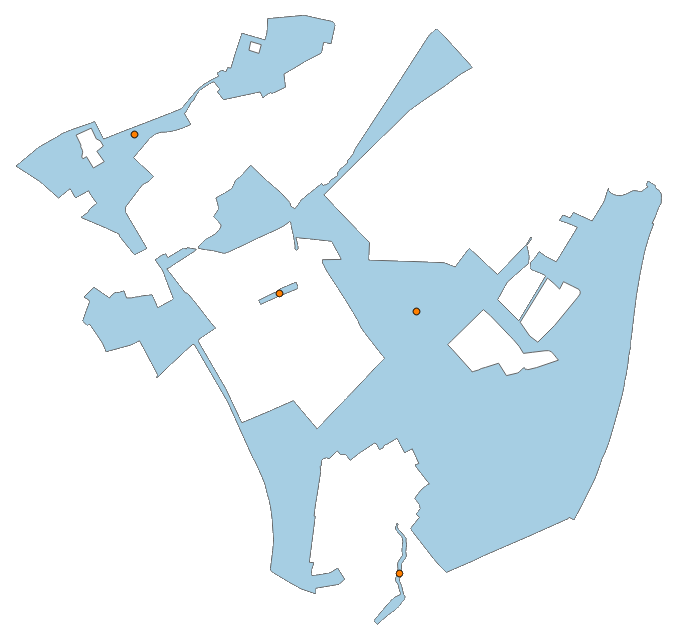
It is also possible to apply the sampler on multi-part polygons:

A multi-part polygon consisting of four parts each sampled by a representative point.

Putting it all together

Based on the knowledge laid out above, it is now possible to furnish the previously created PolygonPointSampler base object with extensions that create sample points by either using the centroid or representative point method. I have called them CentroidSampler and RepresentativePointSampler, respectively:

class CentroidSampler(PolygonPointSampler):
    def perform_sampling(self):
        u"""
        Perform sampling by reprensenting each source polygon with its centroid.
        """
        if not self.prepared:
            self.prepare_sampling()
        for src in self.src:
            self.samples.append(src.centroid)
class RepresentativePointSampler(PolygonPointSampler):
    def perform_sampling(self):
        u"""
        Perform sampling by representing each source polygon with a
        representative point whose coordinates are guaranteed to be within
        the polygon's geometry.
        """
        if not self.prepared:
            self.prepare_sampling()
        for src in self.src:
            self.samples.append(src.representative_point())

 

 

 

Creating sample points in a polygon with OGR and Shapely (Introduction)

Leave a reply

Creating sample points for a given region of interest is a common task in geospatial analysis. It is therefore logically consistent that there is already a number of ways available to create some including the Create Random Points tool of the ArcToolbox in ArcGIS or the corresponding components of the fTools plugin for QGIS. As I’m trying to follow an explicit under-the-hood-philosophy, I will – starting with this very first “real” entry at Portolan – implement my very own sampling methodology for anyone willing to follow.

As it is my (current) programming language of choice I will use Python to accomplish my task. Adding to the fact that I have plenty of working experience with it, Python has the advantage of being very well positioned in the realm of geospatial processing. This is courtesy of a wide range of libraries dealing with corresponding tasks including two that I will use extensively, namely OGR (as part of GDAL) and Shapely. While OGR serves as a well suited toolbox for all things vector – including export and import to external file and/or database formats, basic dataset creation and editing as well as more sophisticated procedures such as generalization – I have found Shapely (basically representing a Pythonic interface to libgeos that is also used by OGR itself) to be a more direct link to the topological operations that are bread and butter for any kind of geographical information system.

As Python explicitly encourages the object-oriented programming paradigm, I will follow that and implement my very own PolygonPointSampler in compliance to that paradigm. Mind you, I’m not an explicitly stated computer scientist, but a cartographer by trait that somehow turned into a mostly self-taught specialist for geoinformatics. My theoretical ramblings with regard to programming may be a little off from time to time, however all of the things presented here do actually work in practice – which is most important for me. And maybe for the reader as well.

Corresponding to these prerequisites a base class for a PolygonPointSampler could be implemented as set out in the following listing:

u"""
A base class for creating sample points located in a given region of interest,
i.e. polygon.
"""

from shapely.geometry import Polygon

class PolygonPointSampler(object):

    def __init__(self, polygon = ''):
        u"""
        Initialize a new PolygonPointSampler object using the specified polygon
        object (as allocated by Shapely). If no polygon is given a new empty
        one is created and set as the base polygon.
        """
        if polygon:
            self.polygon = polygon
        else:
            self.polygon = Polygon()
        self.samples = list()
        self.sample_count = 0
        self.prepared = False

    def add_polygon(self, polygon):
        u"""
        Add another polygon entity to the base polygon by geometrically unifying
        it with the current one.
        """
        self.polygon = self.polygon.union(polygon)
        self.prepared = False

    def print_samples(self):
        u"""
        Print all sample points using their WKT representation.
        """
        for sample_pt in self.samples:
            print sample_pt

    def prepare_sampling(self):
        u"""
        Prepare the actual sampling procedure by splitting up the specified base
        polygon (that may consist of multiple simple polygons) and appending its
        compartments to a dedicated list.
        """
        self.src = list()
        if hasattr(self.polygon, 'geoms'):
            for py in self.polygon:
                self.src.append(py)
        else:
            self.src.append(self.polygon)
        self.prepared = True

    def perform_sampling(self):
        u"""
        Create a stub for the actual sampling procedure.
        """
        raise NotImplementedError