In this edition of our series dedicated to polygon sampling techniques we will look into the process of creating regularly gridded sample points with non-uniform intervals.
Previously published parts of this series include:
Regular grid sampling
Using a single point to represent a whole polygon geometry may satisfy only the most basic sampling demands. Another – and certainly more applicable – way to arrange sample points is to create virtual grids of such points that stretch out over the whole area of the polygon to be processed. To do so we need a regular interval between sample points that may be defined identical (i.e. uniform) in both x- and y-direction. Here we will go the more generic route and implement separately adjustable (i.e. non-uniform) intervals for x and y.
The value range of sample coordinates is of course laid out by the extent of the source polygon. Using Shapely the extent of a polygon is called forth by the property bounds:
>>> from shapely.geometry import Polygon >>> polygon = Polygon([(0,0), (6,0), (0,6)]) >>> print polygon.bounds (0.0, 0.0, 6.0, 6.0)
Given two intervals in x and y it is now easy to create points at regular gridded positions laid out over the extent of the source polygon. Additionally it should be assured that created points are actually within the polygon to be sampled.
>>> from shapely.geometry import Point >>> bounds = polygon.bounds >>> ll = bounds[:2] # lower left coordinate pair of polygon's extent >>> ur = bounds[2:] # upper right ~ >>> x_interval = 1.5 >>> y_interval = 2.0 >>> for x in floatrange(ll[0], ur[0], x_interval): ... for y in floatrange(ll[1], ur[1], y_interval): ... point = Point(x, y) ... if point.within(polygon): ... print point ... POINT (1.5 2) POINT (1.5 4) POINT (3 2)
Now real-world spatial data is different yet again as it rarely comes with extents fitting to full meters. It is still possible to have regularly gridded sample points that have *nicely* looking coordinates by creating extent ceilings and floors used as base for the sampling process. We can actually use our defined intervals to create these values:
>>> from shapely.wkt import loads >>> polygon = loads(open(r"real_world_data.wkt").read()) >>> polygon.bounds (366392.3774440361, 5630693.4900143575, 373404.5164361303, 5641855.842006282) >>> ll = polygon.bounds[:2] >>> ur = polygon.bounds[2:] >>> x_interval = 100 >>> y_interval = 200 >>> low_x = int(ll[0]) / x_interval * x_interval >>> upp_x = int(ur[0]) / x_interval * x_interval + x_interval >>> low_y = int(ll[1]) / y_interval * y_interval >>> upp_y = int(ur[1]) / y_interval * y_interval + y_interval >>> print low_x, upp_x, low_y, upp_y 366300 373500 5630600 5642000
Putting it all together
To extend our previously introduced PolygonPointSampler, we can combine all our findings in a new sub class RegularGridSampler. This one will also make use of the possibility of creating a separate constructor as there is the need to define the sampling intervals.
class RegularGridSampler(PolygonPointSampler):
def __init__(self, polygon = '', x_interval = 100, y_interval = 100):
super(self.__class__, self).__init__(polygon)
self.x_interval = x_interval
self.y_interval = y_interval
def perform_sampling(self):
u"""
Perform sampling by substituting the polygon with a regular grid of
sample points within it. The distance between the sample points is
given by x_interval and y_interval.
"""
if not self.prepared:
self.prepare_sampling()
ll = self.polygon.bounds[:2]
ur = self.polygon.bounds[2:]
low_x = int(ll[0]) / self.x_interval * self.x_interval
upp_x = int(ur[0]) / self.x_interval * self.x_interval + self.x_interval
low_y = int(ll[1]) / self.y_interval * self.y_interval
upp_y = int(ur[1]) / self.y_interval * self.y_interval + self.y_interval
for x in floatrange(low_x, upp_x, self.x_interval):
for y in floatrange(low_y, upp_y, self.y_interval):
p = Point(x, y)
if p.within(self.polygon):
self.samples.append(p)
Using our real-world example and a (uniform) sampling interval of 1,000 meters we arrive at the following result:
We may also use non-uniform sampling intervals of 1,000 meters in x- and 500 meters in y-direction:
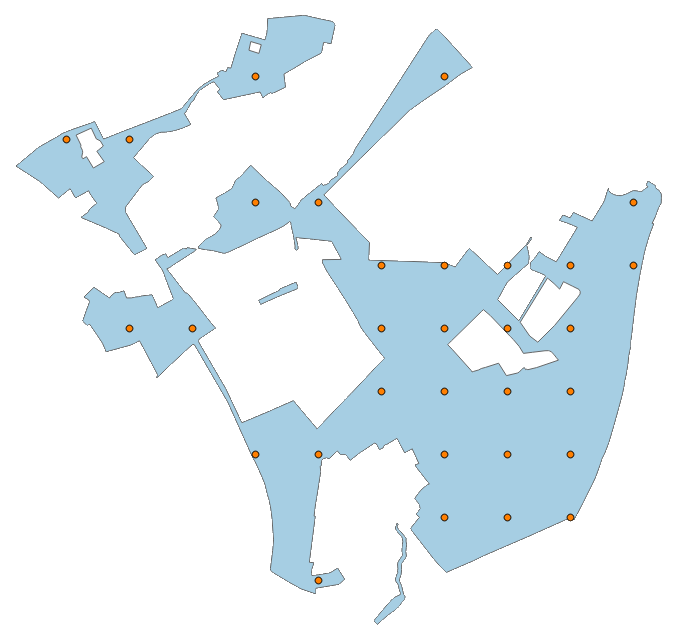
A multi-part polygon may also be used to apply the sampler, for example with a uniform sampling interval of 250 m:
WTH is a floatrange?
In the meantime you most likely have already realized that we’re using a non-standard range function to iterate over a range of float values. Based on a StackExchange suggestion I have defined an according routine in a utility function:
def floatrange(start, stop, step):
while start < stop:
yield start
start += step